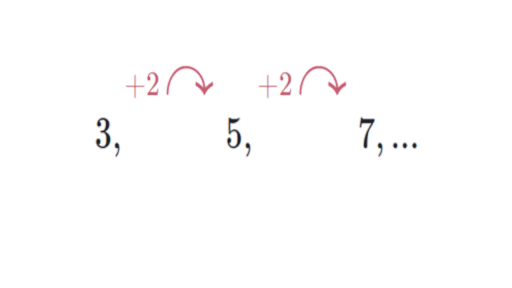Arithmetic Sequence 1 2 3 4 5

It is the 1 st term in the sequence. So the first term is 1 and the last term is 99. Since 100 is even you would really look at the odd numbers 1 99.

apple watch series 5 40mm black apple watch series 3 rose gold case apple watch series 4 golden apple watch series 4 gold milanese loop apple watch series 4 40mm silver apple watch series 4 40mm apple watch series 3 nike plus 44mm apple watch series 5 44mm gold aluminum case with pink sport band

Ppt Number Sequences Powerpoint Presentation Free Download Id 5931322

How To Calculate 1 2 3 4 5 6 7 8 9 10 Quickly Quora

What Is The Next Term Of 1 2 2 3 3 4 And 4 5 Quora

$Grade 10 Math Module 1 Searching For Patterns Sequence And Series$

Grade 10 Math Module 1 Searching For Patterns Sequence And Series

Sequences And Summations In Discrete Mathematics

$Grade 10 Math Module 1 Searching For Patterns Sequence And Series$

Grade 10 Math Module 1 Searching For Patterns Sequence And Series

Is an arithmetic progression with common difference of 2.

Arithmetic sequence 1 2 3 4 5. The next number is found by adding up the two numbers before it. In other words we just add some value each time. This equation was. 1 3 5 7 is the sequence of the first 4 odd numbers and is a finite sequence 4 3 2 1 is 4 to 1 backwards.

This sequence is not arithmetic. Arithmetic sequence arithmetic progression a sequence such as 1 5 9 13 17 or 12 7 2 3 8 13 18 which has a constant difference between terms. The sequence of 1 3 5 7 9 11. The number is changing.

If you know you are working with an arithmetic sequence you may be asked to find the very next term from a given list. The first term is a 1 the common difference is d and the number of terms is n. For example if you have a sequence of 3 5 7 9 the first term will be 3. .

The partial sums of the series 1 2 3 4 5 6 are 1 3 6 10 15 etc the nth partial sum is given by a simple formula. The sequence would be 1 3 5 7 9 etc. For example 5 8 11 14 17 is arithmetic because 8 5 3 11 8 3 and so on. 0 1 1 2 3 5 8 13 21 34.

You should enter 1 on the left side of the first input box and 3 on the right side. An arithmetic sequence is any list of numbers that differ from one to the next by a constant amount. For learning calculations of mean values use mean calculator. In an arithmetic sequence the difference between one term and the next is a constant.

For example the list of even numbers is an arithmetic sequence because the difference from one number in the list to the next is always 2. A sequence is arithmetic if consecutive terms have a common difference. The sum of the first n terms s n of an arithmetic sequence is calculated by the following formula. You may also be asked.

If the initial term of an arithmetic sequence is a 1 and the common difference of successive members is d then the nth term of the sequence is given by. A n a 1 n 1 d. The fibonacci sequence is the series of numbers. For this sequence 1 2 1 1 2 1 3 1 2 1 6 and so on.

User must not confuse it with mean values and significant values.